Implementation
The approach taken to constructing the adjoint is the line-by-line method, where the order of computation is reversed and each line of the tangent-linear (TL) code is transformed into its adjoint form.
This approach is implemented in PSyclone by parsing the tangent-linear code and transforming it into the PSyIR (the PSyclone Internal Representation). A PSyIR visitor has been written that visits each node in the PSyIR tree and transforms each node into its adjoint form. Once this is complete, the PSyIR representation is then written back out as code.
If the supplied tangent-linear code contains active variables that are
passed by argument then the intent of those arguments may change when
translating to their adjoint form. The new intents are determined as a
final step in the visitor for a PSyIR Schedule
node: dependence analysis is used to identify the way in which each
argument is being accessed in the adjoint code and the intent is
updated appropriately.
Active Variables
When creating the adjoint of a tangent-linear code the active variables must be specified. The remaining variables are passive (or trajectory) variables. The active variables are the ones that are transformed and reversed, whereas the passive (trajectory) variables remain unchanged.
Note
it should be possible to only need to specify global variables (ones with a lifetime beyond the code i.e. passed in via argument, modules etc.) as local variables will inherit being active or passive based on how they are used. However, this logic has not yet been implemented so at the moment all variables (local and global) must be specified.
Statements
As the line-by-line method is used then there are rules that must be followed for the different types of statements. This section goes through the rules for each supported statement type.
Assignment
If a tangent-linear assignment statement contains no active variables then it is left unchanged when creating the adjoint code.
If a tangent-linear assignment statement contains one or more active variables then it must be in the following general form:
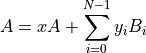
where 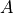 and
and 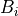 are active variables,
are active variables, 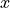 and
and
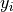 are expressions that do not contain any active variables
and there is no limit on the size of
are expressions that do not contain any active variables
and there is no limit on the size of 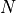 .
.
If this is not the case the associated PSyclone transformation will raise an exception, which will be reported to the user as an error when running the psyad script.
For illustration, consider the case where there are 3 active variables
(equivalent to 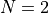 ). We can then write this case in the
following form:
). We can then write this case in the
following form:
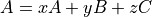
where 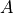 ,
, 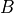 and
and 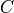 are active variables and
are active variables and
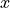 ,
, 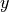 and
and  are expressions that do not contain
active variables.
are expressions that do not contain
active variables.
If the above example is shown in matrix form, we have:
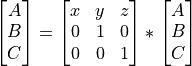
The adjoint of the assignment is obtained by transposing the matrix:
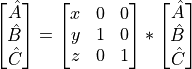
where 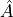 denotes the adjoint of the original active variable
denotes the adjoint of the original active variable 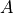 . This gives the
following adjoint assignments:
. This gives the
following adjoint assignments:
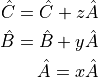
Notice that if the expression 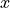 is
is  then the
tangent-linear code writes to
then the
tangent-linear code writes to 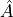 , rather than updating it
i.e.:
, rather than updating it
i.e.:
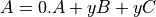
which is:
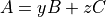
and its adjoint will set 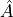 to zero:
to zero:
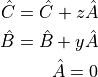
Finally, notice that if 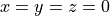 then the original
tangent-linear code sets
then the original
tangent-linear code sets 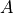 to zero:
to zero:
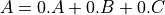
which is:
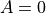
and its adjoint sets 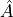 to zero
to zero
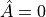
Note
in all cases 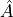 should be written to after it has been
read.
should be written to after it has been
read.
Rules
Rather than creating a matrix and transposing it, it can be seen that there are some relatively simple rules that can be followed in order to create the adjoint of a tangent-linear assignment. This is how the PSyAD AssignmentTrans transformation is implemented. Let’s look again at the previous example tangent-linear statement:
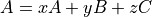
If each of the terms on the right-hand-side (RHS) of the statement are taken in turn
(i.e. 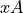 , then
, then 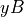 , then
, then 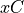 ) there are two cases to consider:
) there are two cases to consider:
the active variable in the RHS term is different to the active variable on the left-hand-side (LHS) of the assignment.
the active variable in the RHS term is the same as the active variable on the LHS of the assignment.
In case 1, the adjoint is simply the active variable on the RHS being updated with the product of its multiplier in the tangent-linear expression with the left-hand active variable. For example, take the case:
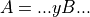
the adjoint for this term is:
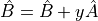
In case 2, the adjoint is simply the active variable being multiplied by the associated term. For the case:
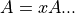
the adjoint for this term is:
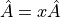
If there is no term for 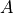 on the RHS of the assignment then the
adjoint variable
on the RHS of the assignment then the
adjoint variable 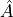 must be set to zero:
must be set to zero:
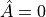
Array Accesses
Active variables will typically be arrays that are accessed within a loop. These can usually be treated in the same way as the scalars illustrated above.
However, in the case of stencils, accesses to different parts of an array in the same statement should be treated as if they were a different variable. For example:
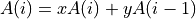
would become:
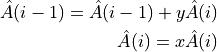
Warning
The authors are not sure that this code is actually correct and it needs to be checked. It might be that all iterations of the first adjoint assignment should be performed before all iterations of the second (i.e. in separate loops).
In LFRic, a kernel is forbidden from writing to data outside the
current column (e.g. to element 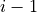 ) and therefore appropriate
transformations will need to be applied to restructure the code.
) and therefore appropriate
transformations will need to be applied to restructure the code.
Limitations
If an active variable is part of the denominator in a division then
the transformation will always raise an exception stating that this
assignment is in an invalid tangent-linear form. For example
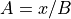 where
where 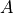 and
and 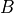 are active
variables. However, if the active variable is within an even number of
divides then it is is, in fact, valid and should not result in an
exception. For example
are active
variables. However, if the active variable is within an even number of
divides then it is is, in fact, valid and should not result in an
exception. For example 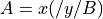 is equivalent to
is equivalent to
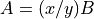 . Issue #1348 captures this current limitation.
. Issue #1348 captures this current limitation.
When zero-ing active variables (see step 1 in the Sequence of Statements (PSyIR Schedule) section) only variables that are scalars or arrays and are of type REAL or INTEGER are currently supported. Issue #1627 captures this limitation.
Transformation
- class psyclone.psyad.transformations.AssignmentTrans(active_variables)
Implements a transformation to translate a Tangent-Linear assignment to its Adjoint form.
- apply(node, options=None)
Apply the Assignment transformation to the specified node. The node must be a valid tangent-linear assignment. The assignment is replaced with its adjoint version.
- Parameters:
node (
psyclone.psyir.nodes.Assignment) – an Assignment node.options (Optional[Dict[str, Any]]) – a dictionary with options for transformations.
Sequence of Statements (PSyIR Schedule)
The PSyIR captures a sequence of statements as children of a ‘Schedule’ node. In PSyclone a sequence of statements in a tangent linear code are transformed to to their adjoint form by implementing the following rules:
1) If there are any active variables that are local to the Schedule in the tangent linear code then they may need to be zero’ed in the adjoint form. The current implementation does not try to determine which local active variables need to be zero’ed and instead zero’s all of them. This approach is always safe but may zero some variables when it is not required. The current implementation sets arrays to zero, it does not use array notation or loops.
2) Each statement is examined to see whether it contains any active
variables. A statement that contains one or more active variables is
classed as an active statement and a statement that does not
contain any active variables is classed as a passive statement.
3) Any passive statements are left unchanged and immediately output as PSyIR in the same order as they were found in the tangent linear code. Therefore the resulting sequence of statements in the adjoint code will contains all passive statements before all active statements.
4) The order of any active tangent-linear statements are then reversed and the rules associated with each statement type are applied individually to each statement and the resultant PSyIR returned.
Note
At the moment the only statements supported within a sequence of statements are assignments and loops. If other types of statement are found then an exception will be raised.
Warning
The above rules are invalid if a passive variable is modified and that passive variable is read both before and after it is modified from within active statements or loops. This case is not checked in this version, see issue #1458.
Loop
The loop variable and any variables used in the loop bounds should be passive. If they are not then an exception will be raised.
If all of the variables used within the body of the loop are passive then this loop statement and its contents is considered to be passive and treated in the same way as any other passive node, i.e. left unchanged when creating the adjoint code.
If one or more of the variables used within the body of the loop are active then the loop statement is considered to be active. In this case:
the order of the loop is reversed. This can be naively implemented by swapping the loop’s upper and lower bounds and multiplying the loop step by
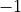 . However, if we consider the following
loop:
. However, if we consider the following
loop: 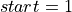 ,
, 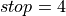 ,
, 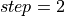 , the
iteration values would be
, the
iteration values would be 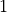 and
and 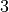 . If this loop is
reversed in the naive way then we get the following loop:
. If this loop is
reversed in the naive way then we get the following loop:
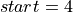 ,
, 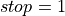 ,
, 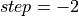 , which gives the
iteration values
, which gives the
iteration values 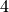 and
and 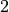 . Therefore it can be seen
that the naive approach does not work correctly in this case. What
is required is an offset correction which can be computed as:
. Therefore it can be seen
that the naive approach does not work correctly in this case. What
is required is an offset correction which can be computed as:
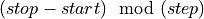 . The adjoint loop start then
becomes
. The adjoint loop start then
becomes 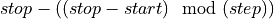 . With this change
the iteration values in the above example are
. With this change
the iteration values in the above example are 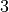 and
and
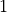 as expected.
as expected.the body of the loop comprises a schedule which will contain a sequence of statements. The rules associated with the schedule are followed and the loop body translated accordingly (see the following section).
Note
if PSyclone is able to determine that the loop step is
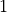 or
or 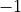 then there is no need to compute an
offset, as the offset will always be
then there is no need to compute an
offset, as the offset will always be  . As a step of
. As a step of
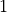 (or
(or 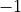 ) is a common case PSyclone will
therefore avoid generating any loop-bound offset code in
this case.
) is a common case PSyclone will
therefore avoid generating any loop-bound offset code in
this case.
If Statement
When an if statement is found in the tangent-linear code, such as the following Fortran snippet:
if (condition) then
! content1
else
! content2
end if
the logical structure of the if is left unchanged, i.e. the
if (condition) then, optionalelseandend if.the sequence of statements within
! content1in the above example, are processed as described in the Section Sequence of Statements (PSyIR Schedule).the sequence of statements within
! content2in the above example, (if it exists, as the else part of an if is optional) are processed as described in the Section Sequence of Statements (PSyIR Schedule).
The condition of the if should only contain passive
variables for this to be a valid tangent-linear code and PSyAD will
raise an exception if this is not the case.
Pre-processing
PSyAD implements an internal pre-processing phase where code containing unsupported code structures or constructs is transformed into code that can be processed. These structures/constructs are detailed below.
Array Notation
Array notation in tangent-linear codes is translated into equivalent loops in the pre-processing phase before the tangent-linear code is transformed into its adjoint. This is performed as the rules that are applied to transform a tangent-linear code into its adjoint are not always correct when array notation is used. Only array notation that contains active variables is translated into equivalent loops.
Intrinsics
If an intrinsic function, such as matmul or transpose, is
found in a tangent-linear code and it contains active variables then
it must be transformed such that it is replaced by equivalent Fortran
code. This is performed in the pre-processing phase.
If an unsupported intrinsic function is found then PSyAD will raise an exception.
The only supported intrinsics at this time are dot_product and
matmul.
If a dot_product or matmul intrinsic is found in the
tangent-linear code it is first transformed into equivalent inline
code before the code is transformed to its adjoint form. The PSyIR
DotProduct2CodeTrans or Matmul2CodeTrans transformations are
used to perform these manipulations. See the
Available transformations section of the user guide for more
information on these transformations.
Note
At the moment all dot_product and matmul intrinsics
are transformed irrespective of whether their arguments and
return values are (or contain) active variables or not.
Note
Note, the transformed tangent-linear code can contain new
variables, some of which might be active. Any such active
variables will need to be specified as active on the PSyAD
command-line using the -a flag even though they do not
(yet) exist in the tangent linear code. Eventually such
variables will be detected automatically by PSyAD, see issue
#1595.
Associativity
As described in the Assignment section, PSyAD expects
tangent-linear code to be written as a sum of products of inactive and
active variables. Therefore if code such as 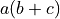 is found
(where
is found
(where 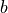 and
and  are active) then it must be transformed
into a recognised form. This is achieved by expanding all such
expressions as part of the pre-processing phase. In this example, the
resulting code is
are active) then it must be transformed
into a recognised form. This is achieved by expanding all such
expressions as part of the pre-processing phase. In this example, the
resulting code is 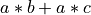 which PSyAD can then take the
adjoint of.
which PSyAD can then take the
adjoint of.
Naming
The generated adjoint code uses modified versions of the module and subroutine names that are used in the tangent linear code.
The modifications are as follows: if the original tangent linear name is prepended with tl_ then this is removed; the tangent linear names are then prepended with adj_.
All adjoint names are also output in lower case, irrespective of the case used in the tangent linear names.
For example, the following tangent linear example:
module tl_example_mod
contains
subroutine tl_example_code()
end subroutine tl_example_code
end module tl_example_mod
would become:
module adj_example_mod
contains
subroutine adj_example_code()
end subroutine adj_example_code
end module adj_example_mod
The Met Office have a convention whereby module names and file names have _mod appended, subroutine names have _code appended and metadata names have _type appended. The approach taken here maintains this convention for the generated adjoint names (as long as the tangent-linear names were also compliant).
Kernel Metadata
In the LFRic API, a kernel is described by its associated Metadata. When creating the adjoint of such a kernel, PSyAD must also update the metadata (since only then can the adjoint kernel be used with PSyclone in a standard fashion). The changes needed are:
Update the name of the associated type and procedure to match the name of the adjointed kernel subroutine;
Update the access mode of each argument passed to the kernel.
Multiple Subroutines
The LFRic API supports mixed precision kernels. It does this by implementing multiple versions of kernel subroutines with different precision and providing a generic interface to them.
Note
Currently such kernels are not supported by PSyAD as the functionality that handles the updating of the associated kernel metadata needs further development.
Test Harness
In addition to generating the adjoint of a tangent-linear kernel, PSyAD is also able to generate a test harness for that kernel that verifies that the generated adjoint is mathematically correct.
This test harness code must perform the following steps:
Initialise all of the kernel arguments and keep copies of them;
Call the tangent-linear kernel;
Compute the inner product of the results of the kernel;
Call the adjoint of the TL kernel, passing in the outputs of the TL kernel call;
Compute the inner product of the results of the adjoint kernel with the original inputs to the TL kernel;
Compare the two inner products for equality, allowing for machine precision.
Steps 1, 3, 5 and 6 are described in more detail below.
Initialisation
All real arguments to the TL kernel are initialised with pseudo-random numbers
in the interval ![[0.0,1.0]](_images/math/95e447259acec74ea23e9547a561a97a219b891f.png) using the Fortran random_number intrinsic
function. If the LFRic API is selected then only real scalar and field arguments
are initialised in this way since arguments such as dof-maps contain
essential information derived from the model configuration. In addition,
those arguments flagged by the user (see Kernel Arguments Containing Geometric Information) as
containing geometric information (i.e. mesh coordinates or panel IDs) are
passed through to the kernel from the Algorithm layer without modification.
Integer and logical scalar arguments are currently just set to 1 and .False,
respectively. This limitation is the subject of issue #2087.
using the Fortran random_number intrinsic
function. If the LFRic API is selected then only real scalar and field arguments
are initialised in this way since arguments such as dof-maps contain
essential information derived from the model configuration. In addition,
those arguments flagged by the user (see Kernel Arguments Containing Geometric Information) as
containing geometric information (i.e. mesh coordinates or panel IDs) are
passed through to the kernel from the Algorithm layer without modification.
Integer and logical scalar arguments are currently just set to 1 and .False,
respectively. This limitation is the subject of issue #2087.
Inner Products
The precision of the variables used to accumulate the inner-product values is set to match that of the active variables in the supplied TL kernel. (An exception is raised if active variables of different precision are found.)
For simplicity, when computing the inner product in steps 3) and 5), both active and passive kernel arguments are included (since the latter will remain constant for both the TL and adjoint kernel calls they can be included in the inner-product compuation without affecting the correctness test). It is likely that this will require refinement in future, e.g. for kernels that have non-numeric arguments.
For the LFRic API, only scalar and field arguments are currently included in the inner-product calculation since operators are never active. (The test-harness generator will return an error if supplied with a TL kernel that writes to an operator.)
Comparing the Inner Products
Performing the comparison of the two inner products while allowing for machine precision is implemented as follows:
Find the smallest possible difference that can be represented by calling the Fortran spacing intrinsic on the largest absolute value of of the two inner products;
Compute the relative difference between the two values by dividing their absolute difference by this spacing;
If this relative difference is less than the overall test tolerance then the test has passed.
By using the largest of the two inner product results in step 1), the resulting spacing value is guaranteed to be appropriate in the case where there is an error and one of the inner products is zero or less than tiny(1.0).
By default, the overall test tolerance is set to 1500.0. This is currently set as a constant in the psyclone.psyad.domain.common.adjoint_utils module but will eventually be exposed as a configuration option (this is the subject of issue #1346). This value is the one arrived at over time by the Met Office in the current adjoint-testing code. In that code, the vector of variables can be of order 200 million in length (since it involves values at all points of the 3D mesh) and therefore there is plenty of scope for numerical errors to accumulate. Whether this value is appropriate for LFRic kernels is yet to be determined.